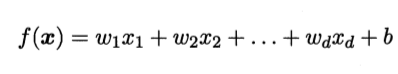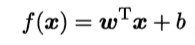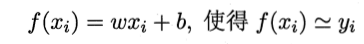基本概念
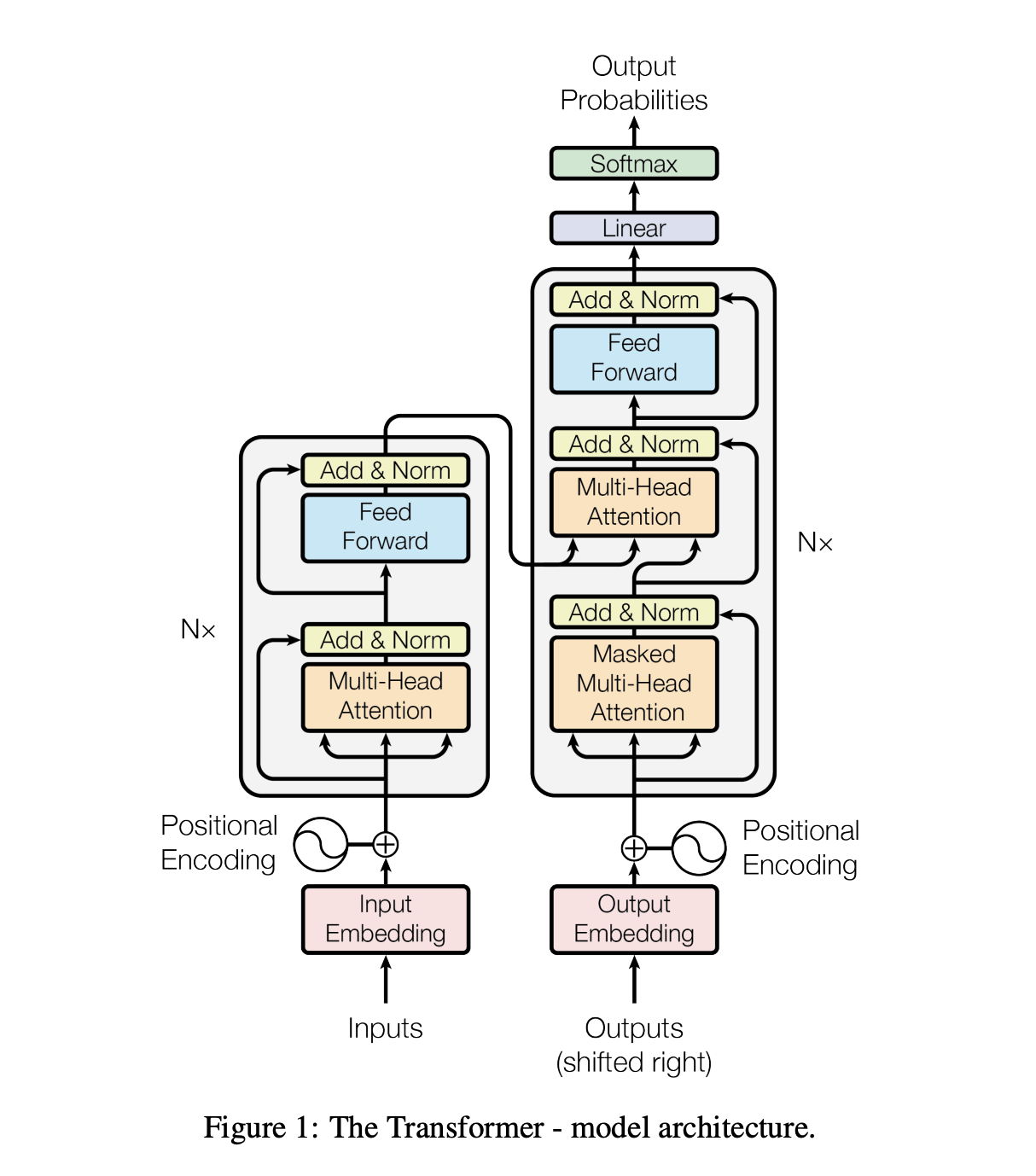
强化学习任务一般通过马尔可夫决策过程(Markov Decision Process, MDP)来描述。
A Markov decision process is a 4-tuple$(S,A,P_a,R_a)$, where
- $S$ is a finite set of states,
- $A$ is the finite set of actions available from state $S$,
- $P_a(s,s^{’})$ is the transfer probability.
- $R_a(s, s^{‘})$ is the immediate reward from state to state s’.
而机器学习的任务便是不断尝试,学习得到一个新的策略(policy)$\pi$。基于这个策略,在不同的状态下选择不同的动作action。有两种表示方法,一种作为函数,一种作为概率表示,表示选择动作的概率。
目标便是长期奖励最大化的策略。常用的是T步累积奖赏。$E[1/T * \sum_{t=1} ^{T} {r_t}]$,或者加上一个累积折扣,即:
$E[\sum_{t=0} ^{+\infty} \gamma^t{r_t}]$
K臂赌博机(K armed bandit)
这是最简单的场景,因为每一步都独立。即只需要最大化单步奖赏。这个情景下,一个动作的奖赏,是一个概率分布,无法通过一次工作得到它的期望奖赏。
这里分为两个阶段,在计算每个臂的期望奖赏时,可以采用仅探索,在知道每个臂的期望奖赏时,采用仅利用,去摇哪个期望奖赏最大的臂。单独使用这两种策略都无法实现奖励的最大化,这时候需要结合两种方式来完成。
$\epsilon$-贪心
算法对两种方法取折中,即按照概率确定选用哪个策略,再进行摇臂。有一个优化就是,前期更倾向于探索,后期更倾向于利用,即根据步数修改$\epsilon$。
softmax
算法基于期望奖赏,分配摇臂的概率,按照概率选择哪个臂。摇臂概率大分布按照Boltzmann分布。
$$
P(k) = \frac{e^\frac{Q(k)}{\tau}}{\sum e^{\frac{Q(i)}{\tau}}}
$$
二者对比
具体选择哪个取决于具体应用,也与选择的参数有关系,例如$\tau$, 越小,则趋向于仅利用
有模型学习
假设,MDP过程的四元组已知,便认为是模型已知,即机器已经对环境建模。对于这种情况,成为有模型学习。
策略评估
在模型已知的情况下,策略$\pi$的累积奖赏便可以估计得到。
$V^\pi(x)$表示,在x的初始状态下,基于$\pi$策略的累积奖赏。称为状态值函数(state value funciton)
$Q^\pi(x, a)$表示 x作为初始状态,执行动作a后,带来的累积奖赏。称为:状态动作值函数。(state action value function)
根据累积奖赏的两种定义,可以得到:
$$
V_T^\pi(x) = E_\pi[1/T \ * \sum_{t=1}^{T}r_t|x_0 = x], \ \ \ \ \ T步累积奖赏
$$
$$
V_T^\pi(x) = E_\pi[\sum_{t=0}^{+\infty}\gamma^tr_{t+1}|x_0 = x], \ \ \ \ \ \gamma 折扣累积奖赏
$$
状态动作值函数为:
$$
Q_T^\pi(x,a) = E_\pi[1/T \ * \sum_{t=1}^{T}r_t|x_0 = x, a_0=a], \ \ \ \ \ T步累积奖赏
$$
$$
Q_T^\pi(x,a) = E_\pi[\sum_{t=0}^{+\infty}\gamma^tr_{t+1}|x_0 = x,a_0=a], \ \ \ \ \ \gamma 折扣累积奖赏
$$
基于马尔可夫性质,可以将公示写为递归的形式。
$$
V_T^\pi(x) = E_\pi[1/T \ * \sum_{t=1}^{T}r_t|x_0 = x] \
= \sum\pi(x, a)* \sum_{x\in X}(P_{x\rightarrow x^{‘}} * (\frac{1}{T} * R_{x\rightarrow x{‘}} + \frac{T-1}{T}* V_T^\pi(x^{‘})))
$$
同理,$\gamma$折扣累积奖赏也有如下的累积递归公式。
$$
V_T^\pi(x) = \sum\pi(x, a)* \sum_{x\in X}(P_{x\rightarrow x^{‘}} * (R_{x\rightarrow x{‘}} + \gamma * V_T^\pi(x^{‘})))
$$
可以看到,只有当状态转移矩阵P和奖赏矩阵R已知的前提下,才能完全展开。