线性模型
1.基本形式
线性模型的基本思想是通过属性或者特征的线性组合来预测的函数. 数学表达如下:
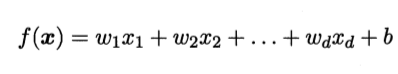
更通俗的向量表达为:
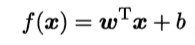
线性模型比较简单, 并且具有较好的解释性. 很多非线性模型实际上是通过将特征映射到高维空间当中或者通过引入层级结构来实现非线性模型.
经典的线性模型有: 线性回归, 逻辑回归.
2. 线性回归
基于已有数据集 D = {(x1, y1 ) …, (xm, ym )}, 其中x为向量, 表示特征集合. y为实数. 线性回归会取学习到一个线性模型, 使得根据特征向量x, 可以尽可能精确的预测y.
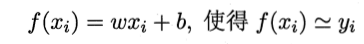
为了确定模型中的参数w, b. 我们首先需要找到一个模型的性能度量. 在回归任务当中, 比较常用的衡量指标是: 均方误差. 这样, 目标函数便是最小化均方误差, 也叫做最小二乘法.
均方误差具有较好的几何意义, 它对应了常用的欧几里得距离.
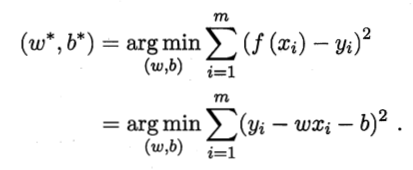
求解w和b的上述过程, 叫做 线性回归模型的最小二乘 “参数估计”. 由于上述函数是关于w和b的凸函数(这个地方我很好奇 为什么不是叫凹函数,从文字象形上来说 更像凹形状), 因为有这样的性质, 直接求导, 导数为0的点必是最优解, 也是上述函数的最小值点.
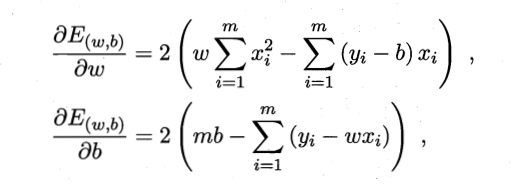
解得:
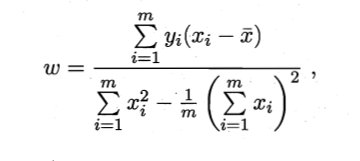
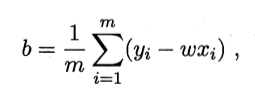
计算机中, 利用矩阵可以通过并行计算加速, 矩阵形式的表示的求解如下:
首先为了计算, 做一点变化, 首先在x的特征向量当中添加一个常数项 1, 这样可以让b 添加w中.即:
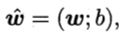
于是, 矩阵表示的目标函数为:
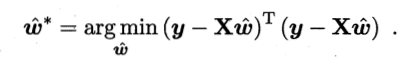
对w求导可以得到:
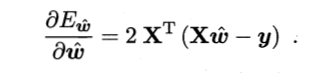
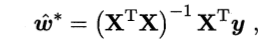
实际情况是, 由于样本数量较多, 并且 有误差的存在, XTX不是满秩矩阵, 这个时候可以通过引入正则化变量
最后说一下广义线性模型, 即在输出的结果中, 使之成为一个可微函数的的输入.
3.逻辑回归
i 模型表示
上述线性回归返回的是一个连续值, 那么在做进行分类任务的时候, 需要将连续值转换为0/1值.
可以想到的是单位阶跃函数, 和 sigmoid函数. 这里利用广义线性模型, 将求得的连续值作为可微函数输入.
由于单位阶跃函数不可微, 所以一般都会选择sigmoid函数, 将输出的值, 记作z 转换为0 -1 之间的连续值.
sigmoid函数可以表示为:
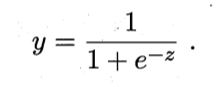
最后输出可以表示为:

ii 目标函数(损失函数)
经过转换后, 我们可以将y的值看作样本为正例的概率, 将1 - y 看作样本为负例的概率. 然后通过”极大似然法”来对参数w和b进行估计.
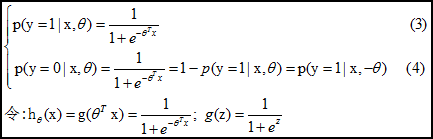
这里用theta将w和b 一起表示
单个样本的概率表示为:
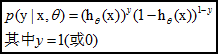
极大似然函数为:
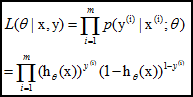
取对数后:
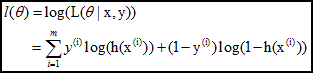
结果就是要最大话上面的公式, 最大化和最小化是等价的, 但一般都会选择转化为最小化. 也就是在上述公式前面添加负号.
iii 通过梯度下降求解
要使得最小化下面公式:
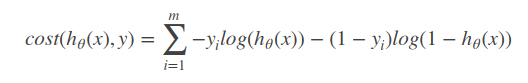
采用梯度下降的方式完成.
此时通过链式求导, 并且注意利用性质:
g(z)的导数为: g(z)*(1 - g(z))
手工求解如下(这个地方用到损失函数多求了一个平均):
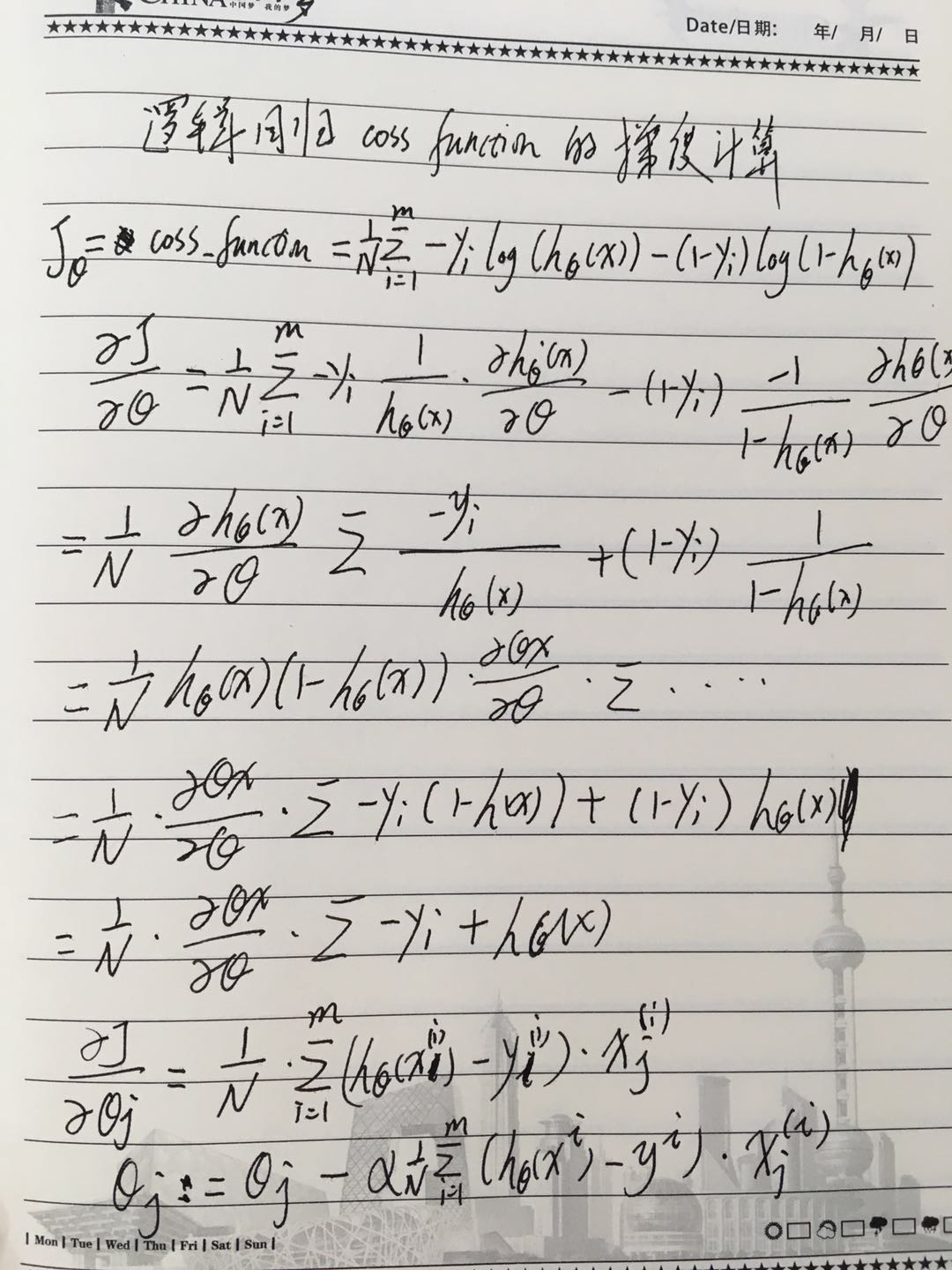
其中, a为学习率, 当模型训练无法收敛时, 可以尝试将学习率调小
iiii 正则化
在目标函数中, 为了防止过拟合, 一般会加入正则项.
通常选用的正则项为L1正则和L2正则.
这两种正则化的区别是L1正则可以更容易产生稀疏解.
4.其它
逻辑回归是一种判别模型, 直接对P(y|x)建模. 生成式模型则是对数据的联合分布建模. 通过贝叶斯公式计算个类别的后验概率, 即:
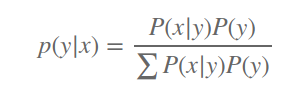
事实上, 当P(x|y)的分布属于指数分布族时, 可以将生成式推导到判别式模型.